상트페테르부르크의 역설(St. Petersburg Paradox)은 수학자 니콜라스 베르누이(Nicolaus) Bernoulli)가 낸 게임과 관련된 역설이다.
상트페테르부르크(지금은 레닌그라드)라는 이름이 붙은 것은 한 때 상트 페테르부르크에서 강의를 했던 그의 사촌인 다니엘 베르누이(Daniel Bernoulli)가 상트 페테르부르크라는 이름이 들어간 학술지에 그 해결책을 기고했기 때문이라고 한다.
이 역설은 투자에 주는 의미도 있는데 역설의 내용과 해결 과정을 알게되면 그 의미도 알 수 있게 된다.

상트페테르부르크의 역설: 게임 참가 또는 투자를 할 때 기대 수익만 고려할까?
베르누이가 낸 문제는 다음과 같은 게임 규칙이 있을 때 어느 정도의 참가비여야 사람들이 게임이 참가할 것인가였다. 수학자가 낸 문제지만 문제 자체는 복잡한 수학을 포함하고 있지는 않다.
[게임 규칙]: 동전을 앞면이 나올 때까지 던진다. 첫 번째 시도에서 앞면이 나오면 상금 2원을 받는다. 첫 번째 시도에서는 뒷면이 나오고 두 번째 시도에서 앞면이 나오면 상금 22원을 받고, 첫 번째와 두 번째 시도에서 뒷면이고 세 번째 시도에서 앞면이 나오면 상금 23원을 받는다. 이런 식으로 해서 n번째 시도에 앞면이 나온다면 상금 2n원을 받을 것이고, 앞면이 나올 때까지 시도는 무한정 할 수 있다.
잃어도 되는 돈으로 재미 삼아 게임을 하려는 것이 아니라면, 사람들은 참가비가 대략 기대 수익과 비슷하거나 낮아야 참가하는 것이 보통이다.
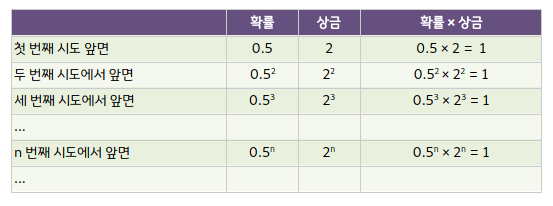
게임의 기대 수익은 각 상금에 그 상금을 받을 확율을 곱한 금액을 모두 더한 금액이다. 앞면이 나오지 않는한 무한정 게임을 할 수 있는 이 게임의 기대수익은 아래 표를 참고하면 ‘1 + 1 + 1 + …’로 무한대다.
기대 수익이 무한대인데…, 당신이라면 참가비가 단돈 천 원이라고 해도 위 게임에 참가하겠는가?
이 게임에서 1천 원 이상의 상금을 받으려면 최소한 9번 째까지 뒷면이 계속해서 나오다가 10번 째에서 앞면이 나와야 한다. (10번 째에 앞면이 나오면 상금은 210=1,024원 임.) 그러나 동전에 이상이 없다면 9번 째까지 뒷면이 계속해서 나오다가 10번 째에 앞면이 나오는 일은 흔하지 않은 일이다.
이 게임은 첫 번째 시도에서 뒷면이 나오고 연속해서 뒷면이 나올수록 참가자에게 유리한 게임이다. 앞면이 나오는 순간 게임은 끝나지만, 앞면이 늦게 나오면 나올수록 상금은 높아진다.
기대 수익(∞)만 본다면 이 게임은 전 재산을 걸고라고 참가해 볼 만하다.
그러나 당신이 첫 번째 시도에서 앞면이 나올 것이라고 기대한다면 참가비가 1원이라고 해도 참가가 망설여 질 것이고, 두 번째 시도에서 앞면이 나올 것이라고 기대한다면 참가비가 2원이라도 참가비가 비싸다고 생각할 것이다.
상트페테르부르크의 역설은 게임의 기대 수익이 엄청나게 높지만 참가비가 현저하게 낮지 않은 이상 사람들이 게임에 참가하지 않으려는 현상이다. 그런데 사람들이 왜 이 게임의 참가비가 낮아야 한다고 생각하는 걸까?
상트페테르부르크 역설의 해결과 투자의 원칙
수학적인 해결은 적절한 참가비를 찾는 것이었는데, 이 역설이 이름 붙게 된 계기가 된 다니엘 베르누이도 해결책을 내 놓았고, 그 보다 앞서 가브리엘 크래머(Gabriel Cramer)라는 수학자도 해결책을 내 놓았다.
둘 다 효용 개념을 이용했는데, 적절한 참가비를 정하기 위해서는 동전을 던지는 횟수가 늘어날수록 사람들이 느끼는 만족도인 효용(utility)을 고려해야 한다는 것이었다.
앞면이 나올 때까지의 횟수가 늘어날수록 상금이 늘어나기 때문에 효용은 늘어나겠지만, 횟수가 늘어날 수록 위험 또한 커지기 때문에 늘어나는 효용의 정도는 줄어든다. 말하자면 앞면이 나올 때까지의 횟수가 늘어날 수록 총효용(total utility)은 증가하지만 마지막 한 단위의 효용인 한계 효용(marginal utility)은 줄어든다(체감한다).
크래머는 한계 효용이 체감 하는 효용 함수로 무리 함수를 제안했다. 상금을 W라고 하면, 크래머의 효용 함수는 U(W)=W1/2로 표현된다. 이 효용 함수로 각 회차 마다의 효용을 계산한 후 확률을 곱하여 각 회차의 기대 효용을 계산한 후 모두 더하면 다음과 같다. 기대효용=0.51/2 + 0.52/2 + 0.53/2 + ….
위 기대효용은 초항과 공비가 모두 0.51/2인 무한 등비 수열의 합과 같은데, 공식{초항 ÷ (1-공비)}을 적용하면 이 게임의 기대 효용은 2.42원 정도 된다.
이 게임의 기대 효용가 같은 정도의 효용을 주는 금액을 참가비로 정한다면, U(참가비)=참가비1/2=2.42원에서 참가비를 계산하면 약 5.83원 이다. 참가비가 최대 6원 미만이어야 사람들은 비로소 이 게임에 참가하게 된다는 이야기가 된다.
기대 수익에 비하면 참가비는 아주 미미한 금액인데, 이렇게 참가비가 낮은 것은 이 게임의 기대 효용이 낮기 때문이고, 기대 효용이 낮은 건 기대 수익도 높지만 기대 수익을 얻지 못할 위험도 높기 때문이다.
상트페테르부르크의 역설의 해결은 투자에 주는 의미도 있다. 바로 기대 수익이 높다고 혹할 것이 아니라 투자에 내재한 위험도 고려해야 한다는 것이다.